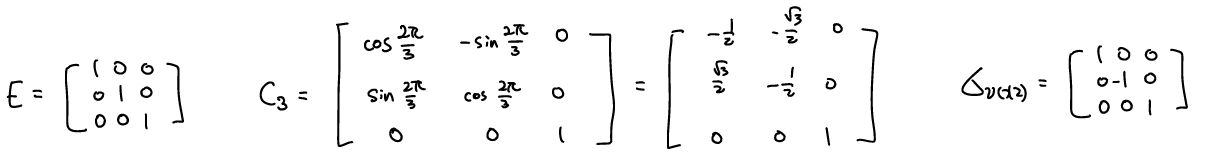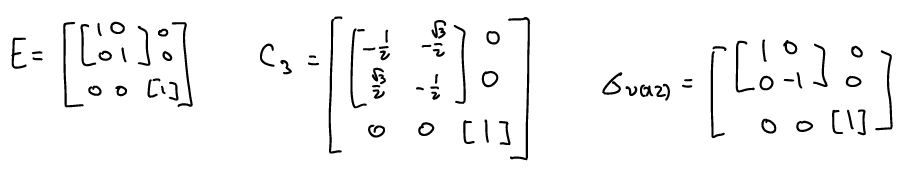Point Groups
한 분자의 여러 symmetry operations을 하나의 set로 모아놓은 것 을 그 분자의 point group이라고 한다.
Point group을 결정하는 것은 아래의 diagram을 따라가기만 하면 된다. 다만 첫번째 step인 분자가 low (or high) symmetry를 가지고 있느냐만 집고 넘어가보자.
low symmetry는 symmetry가 없거나(E), 하나의 mirror plane (Cs)만 있거나, 하나의 inversion center (Ci) 만 있을 경우에 해당된다.
high symmetry는 여러가지가 있는데,
C∞υ: linear하고, inversion center가 없는 경우, HCl
D∞h: linear하고 perpendicular C2 axis, perpendicular mirror plane, inversion center가 존재하는 경우, CO2
Td: Tetrahedral, CH4
Oh: Ohtahedral, SF6
Ih: Icosahedral, B12H122-
주의: perpendicular C2 axis가 없으면 (C가 아니고) D group!
Matrix representation
각각의 symmetry operation은 행렬의 형태로 표현할 수 있는데, 이를 transformation matrix라고 한다.
[New coordinates] = [transformation matrix] [old coordinates]
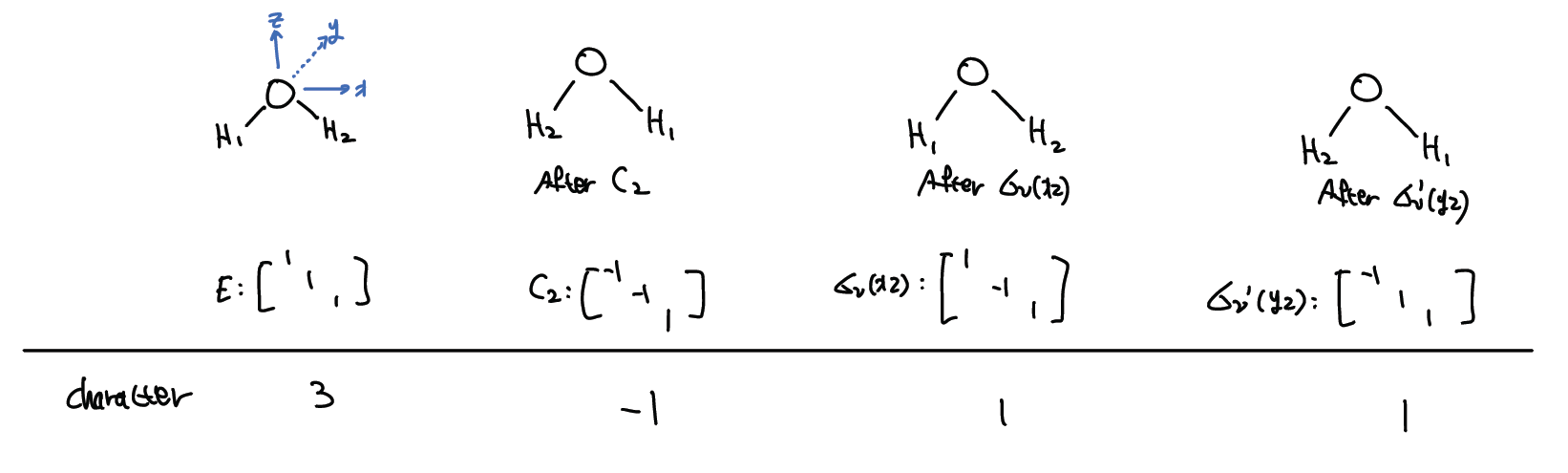
H2O (C2υ)를 예로 들어보자. 물분자는 세개의 atom이 있고, 따라서 각 atom마다 xyz coordinate가 있다. 물분자에는 네 개의 symmetry operations이 있다. 이중에서 어떤 operation을 몇 번을 하든 원래의 물분자와 indistinguishable 하다.
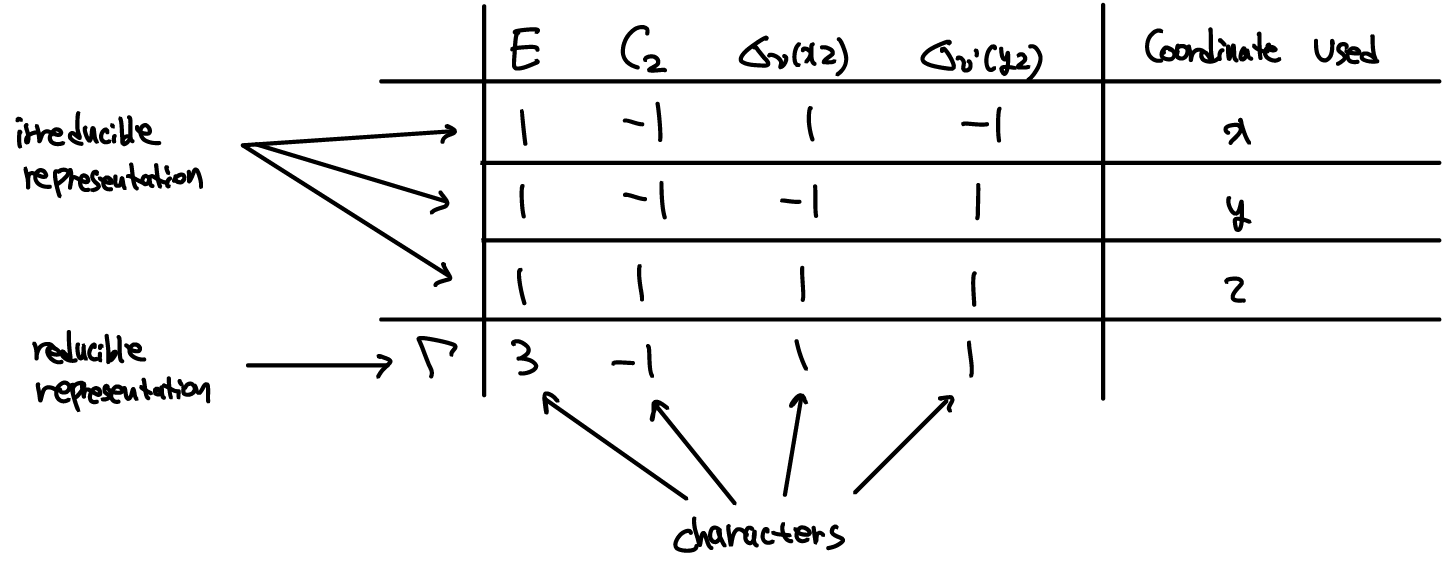
Character 란 위의 예시처럼 diagonal에 있는 요소들의 합을 말한다. 이런 character들의 집합을 reducible representation (Γ) 이라고 한다. C2υ의 경우 각 symmetry operation의 matrix representaion은 diagonal element를 제외하면 모두 0 이기 때문에, 각 matrix를 3개의 digonal 1x1 block matrix로 나눌 수 있고, 각 block matrix의 digonal element의 합(여기서는 1)을 각 operation의 column에 써줄 수 있다. 이때 각 row 를 irreducible representation 이라고 한다.
따라서 block diagonalize 하기 전의 matrix의 charater들의 집합은 reducible representation (Γ) , block diagonalize 한 후의 각 block의 charater들의 집합을 irreducible representation 이라고 생각하면 편하겠다.
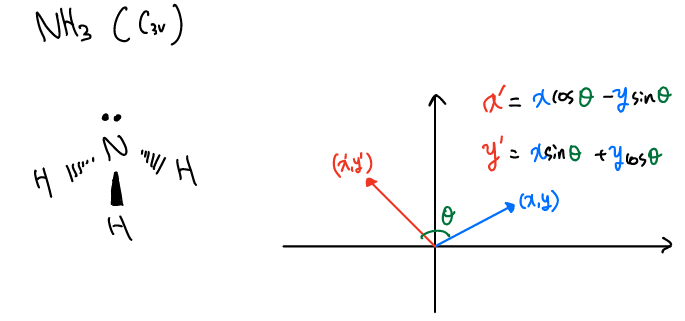
Let’s make a character table for NH3 molecule
NH3는 C3υ point group으로 C3υ는 C3를 principal axis로 두 번 회전가능하고 (2C3), 3개의 συ plane이 (3συ) 있다.
(x,y) 좌표를 θ만큼 회전시켰을 때 (x’,y’)은 위와 같은 관계가 있으므로 E, C3υ, συ(xz)를 transformation matrix로 아래와 같이 나타낼 수 있다.
그런데 이 때, C2υ의 경우와는 달리, off-diagonal element가 0이 아닌 matrix (C3υ)가 있으므로, C3υ를 최소한으로 block diagonalize할 수 있는 방법은 아래와 같이 2x2 와 1x1 행렬 두 개로 나누는 방법 밖에 없다. 따라서 나머지 operation들도 이와 같이 나누면,
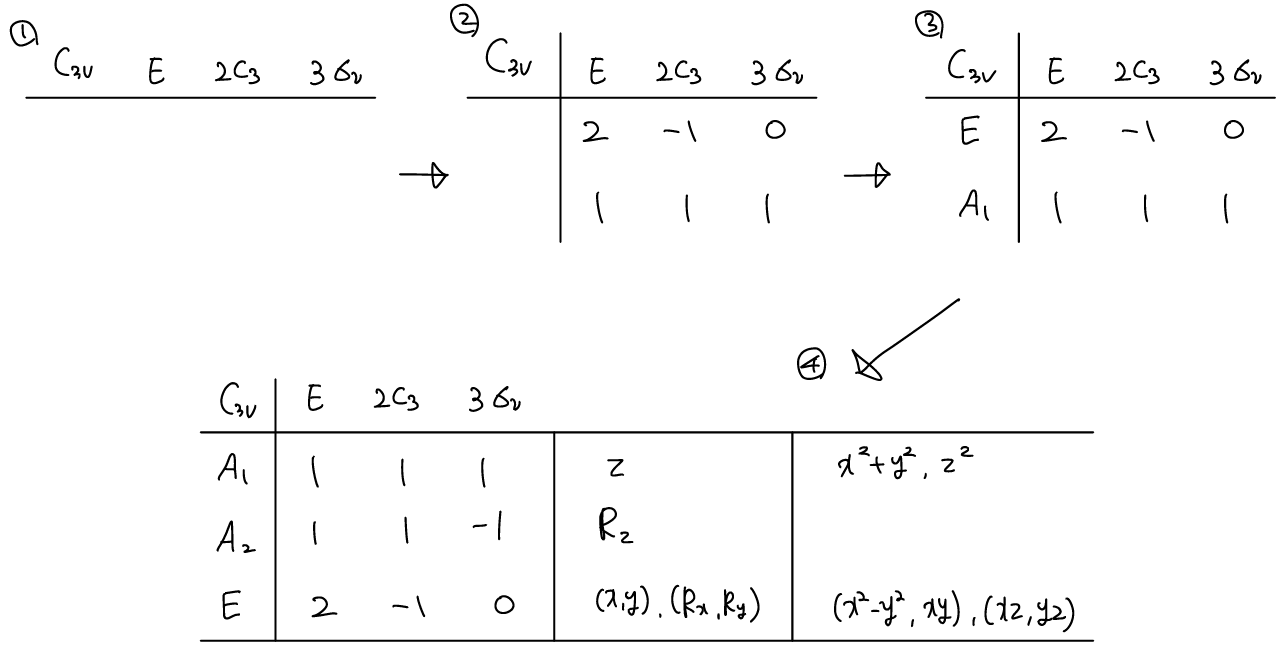
C3υ의 charater table을 만들기 위해,
- operation들 나열
- 각 operation에 속해있는 block matrix들의 character (digonal element들의 합) 써주기.
- 각 irreducible representation에 label 붙이기.
- class는 3개인데, irreducible representation은 두개 밖에 없으니 나머지 하나 (A2) 찾은 후 label 순서대로 나열해주기.
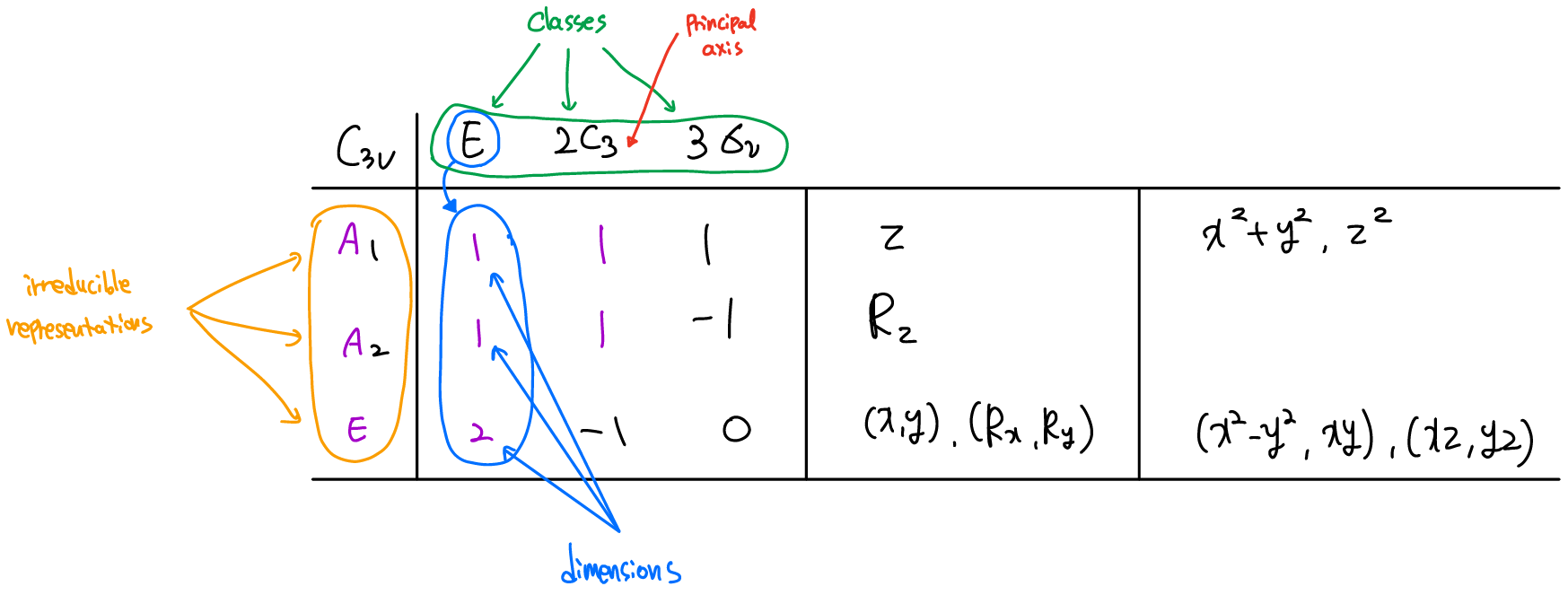
Charater table을 볼 때, order: 6 = 1(E)+2(C3)+3(συ), class, dimension 등등이 헷갈리지 않도록 잘 기억해 두도록 하자.
irreducible representation은 아래와 같은 규칙으로 notation 한다..