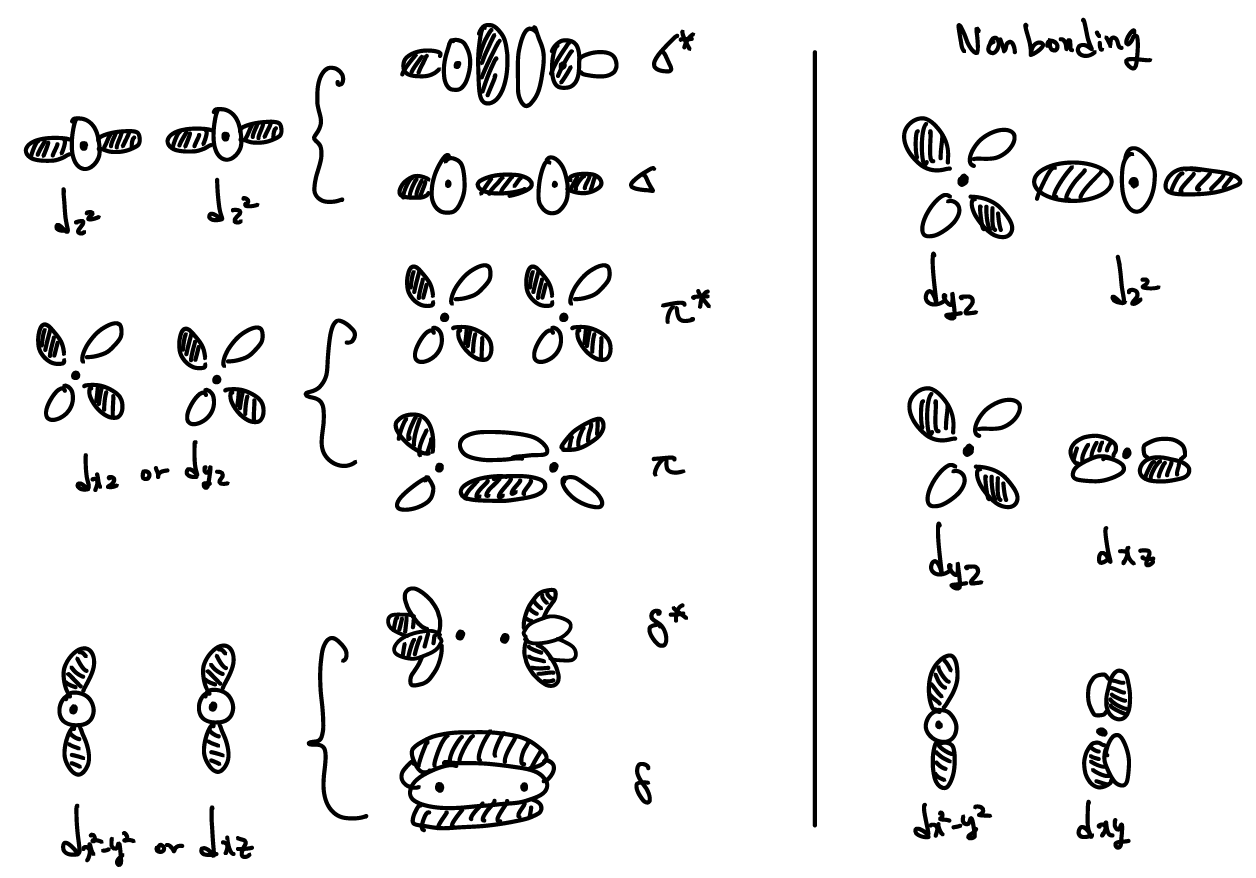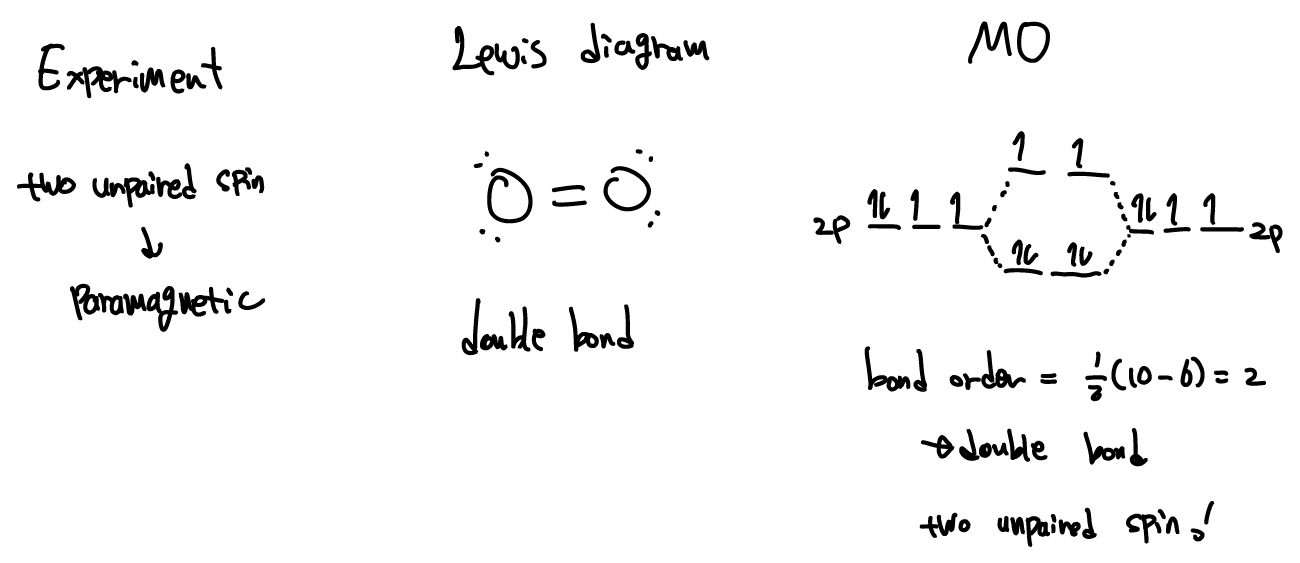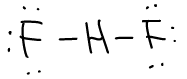Molecular orbitals from atomic orbitals
분자의 Schrödinger equation을 풀면 대략적인 solution으로서 linear combination of the atomic orbitals (LCAO)를 구성할 수 있는데, LCAO란 원자의 wavefunction의 합 또는 차이다. H2를 예로 들면,
\(\Psi=c_{a} \psi_{a}+c_{b} \psi_{b}\)
여기서 𝚿는 molecular wave function이고, 𝝍a, 𝝍b는 atomic wave function이다. ca, cb는 조정이 가능한 계수로 양수 또는 음수가 될 수 있고, 두 값이 같거나 다를 수도 있다. 두 원자간의 거리가 가까워질수록 orbital이 서로 overlap되며 molecular orbital을 구성할 수 있게 된다. bonding을 구성하는 조건으로 다음의 세가지를 들 수 있다.
- 두 orbital symmetry의 sign이 같아야 한다.
- 두 atomic orbitals의 에너지가 서로 비슷해야한다.
- 두 원자간의 거리가 적당히 가까워야 한다.
Molecular orbitals from s orbitals
아래는 Ha, Hb를 가진 H2 분자의 molecular orbital (MO)이다.
\(\begin{aligned} \Psi(\sigma) &=N\left[c_{a} \psi\left(1 s_{a}\right)+c_{b} \psi\left(1 s_{b}\right)\right]=\frac{1}{\sqrt{2}}\left[\psi\left(1 s_{a}\right)+\psi\left(1 s_{b}\right)\right]\left(\mathrm{H}_{a}+\mathrm{H}_{b}\right) \\ \Psi\left(\sigma^{*}\right) &=N\left[c_{a} \psi\left(1 s_{a}\right)-c_{b} \psi\left(1 s_{b}\right)\right]=\frac{1}{\sqrt{2}}\left[\psi\left(1 s_{a}\right)-\psi\left(1 s_{b}\right)\right]\left(\mathrm{H}_{a}-\mathrm{H}_{b}\right) \end{aligned}\)
여기서 Atomic orbital(AO)의 부호(sign)는 임의적이다.
Bonding MO는 두 AO의 합으로 두 원자핵 사이의 electron concentration을 증가시키고, 에너지를 낮다.
Antibonding MO는는 두 AO의 차로 두 wave function의 상쇄로 인해 zero electron density, 즉 node가 생기고, 에너지가 높다. 이러한 antibonding MO의 electron은 두 원자 사이에 반발력을 일으킨다.
Nonbonding orbital도 가능한데, 한 원자의 AO symmetry가 다른 원자의 AO symmetry와 맞지 않거나, 우연히 MO의 에너지가 AO의 에너지가 같은 경우이다.
어떤 상황에서든 MO의 수는 AO의 수와 같다.
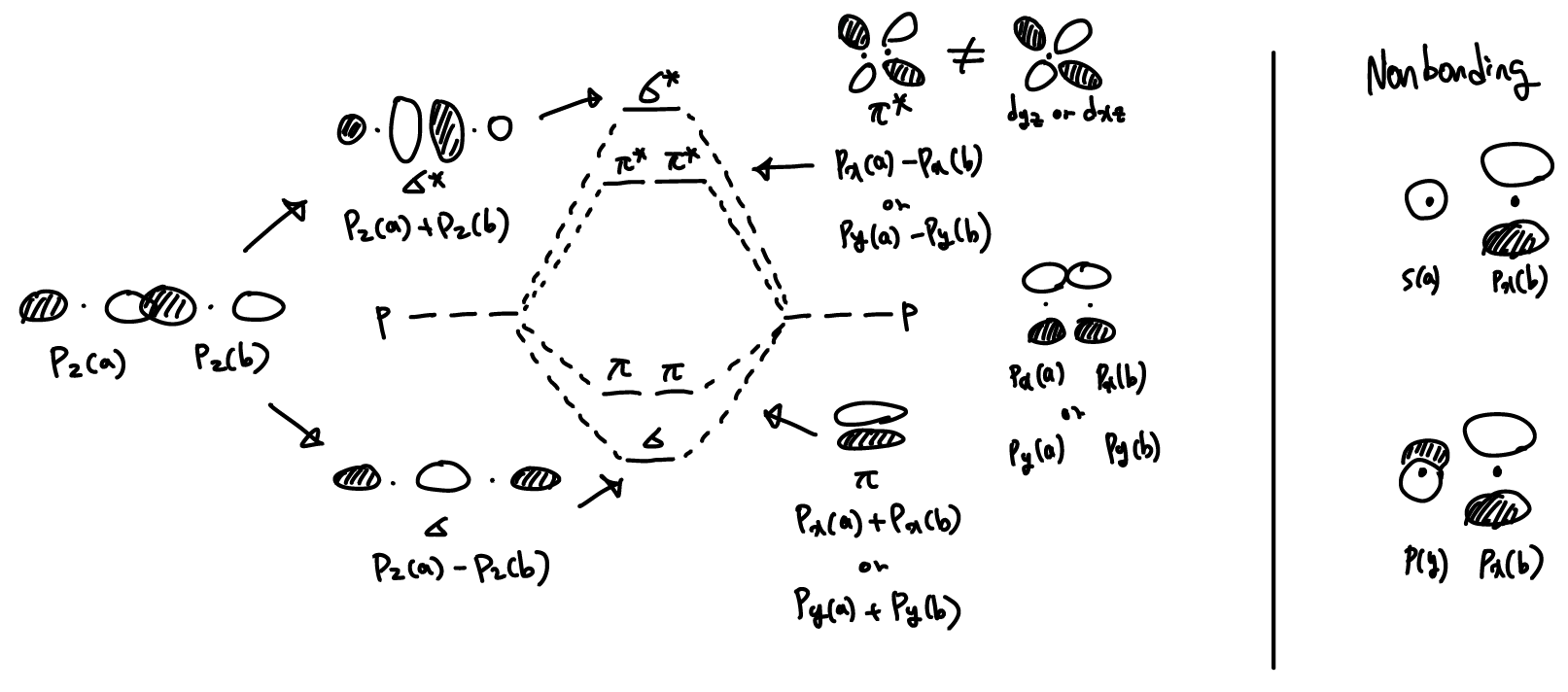
Molecular orbitals from p orbitals
두 원자핵을 연결하는 축을 z축으로 정의하자. 이 경우 pz orbital끼리 빼야, σ orbital을 이루고, 더하면 σ* orbital을 만든다.
같거나 반대의 sign을 가진 orbital overlap의 기여가 같으면, bonding과 antibonding의 효과가 상쇄되어 MO를 만들지 않는다. 즉, 한 원자의 AO symmetry properties가 다른 원자의 어떠한 AO와도 맞지 않으면(do not match), nonbonding orbital 이라고 한다.
Molecular orbitals from d orbitals
bonding notation
| notation | symmetry | # of nodes that include the center of bond axis |
|---|---|---|
| σ(sigma) | symmetric to rotation about bond axis | 0 |
| π(pi) | change in sign with C2 rotation | 1 |
| 𝛿(delta) | change in sign with C4 rotation | 2 |
Molecular orbitals
Lewis electron-dot diagram을 이용하면 N2, O2, F2와 같은 분자들은 큰 문제가 없지만, Li2, Be2, B2, C2와 같은 분자들은 octet rule을 만족시키지 않기 때문에 설명하기 어렵다. 게다가 O2는 실험적으로 두개의 unpaired electrons이 관측되고 따라서 paramagnetic 성질을 보이는데 Lewis 방식으로는 이를 설명할 수 없으므로 Molecular orbital이 필요하다.
bond order
bonding과 antibonding electrons의 수는 bond의 수를 결정하는데, 이를 bond order 라 한다.
Bond order = 1/2*{(# of e- in bonding orbitals)-(# of e- in antibonding orbitals)}
O2를 예로들면 1/2*(10-6) = 2 로 Lewis electron-dot diagram의 경우와 같이 double bond를 나타낸다.
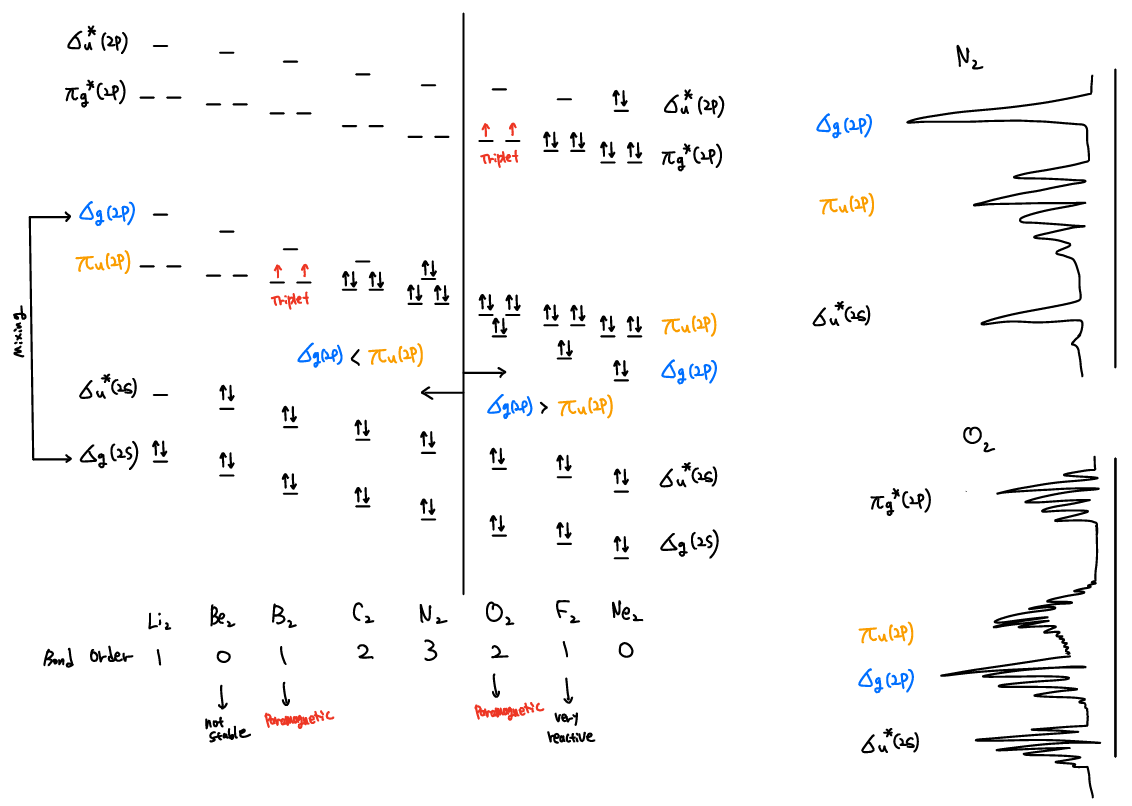
Orbital Mixing
같은 symmetry를 가진 두 개의 MO 이 비슷한 에너지를 가질 때, 이 둘은 서로 상호작용하여 낮은 orbital의 에너지를 더 낮추고, 높은 orbital의 에너지는 더 높인다. 아래의 homonuclear diatomics의 예를 보면, σg(2s) 와 σg(2p) 는 같은 σg symmetry를 가지고 있고, 서로 상호작용하여 σg(2s) 의 에너지를 낮추고 σg(2p) 의 에너지를 높인다. 비슷하게, σu* 끼리도 상호작용하여 σu* (2s) 의 에너지를 낮추고, σu* (2p)의 에너지를 높인다.
이 네 개의 MO 를 비슷한 에너지를 가진 네 개의 AO의 combination으로 다음과 같이 나타낼 수 있다.
\(\Psi=c_{1} \psi\left(2 s_{a}\right) \pm c_{2} \psi\left(2 s_{b}\right) \pm c_{3} \psi\left(2 p_{a}\right) \pm c_{4} \psi\left(2 p_{b}\right)\)
Homonuclear molecules의 경우 c1=c2, c3=c4 이다. 이 네 개의 MO 는 mixing을 하지 않았을 때와 symmetry는 같지만, s와 p character의 mixing 때문에 모양은 좀 달라진다.
Homonuclear Diatomic Molecules
먼저 magnetism에 대한 정리부터 시작해보자.
Diamagnetism: unpaired electron이 없고, magnetic field에 대해 아주 적은 양만큼 척력이 작용함.
Paramagnetism: unpaired electron이 작은 자석처럼 작용하여 외부 magnetic field에 대해 인력이 작용하지만 magnetic field가 있을 때만 magnetized 됨.
Ferromagnetism: magnetic field로 인해 유도된 magnetism이 field가 사라져도 유지됨.
Homonuclear diatomic molecule의 경우를 보자. 같은 symmetry를 갖는 σg(2s) 와 σg(2p) 가 Mixing 하여 σg(2p)의 에너지는 올라가고, σg(2s)의 에너지는 내려간다. 따라서 nuclear charge (Z)가 작을 때는 σg(2p)의 에너지가 πu(2p)의 에너지보다 높아진다. Z가 커질수록 σ orbital의 에너지가 π orbital 보다 더 크게 낮아지게 되는데, 이는 σ interaction에 참여하는 atomic orbital의 overlap이 더 크기 때문이다. 또한 2s orbital이 2p 보다 shielding effect가 적기 때문에 Z가 커질수록 더욱 크게 안정화되고, 2s와 2p간의 에너지차이가 심해지면서 mixing이 적어지고 따라서 σg(2p)의 에너지가 πu(2p) 보다 낮아지게 된다.
MO theory에서는 Mixing 통해, 위의 그림처럼 B2 와 O2 가 Paramagnetic 성질을 갖는 지, C2가 어떻게 σ bond 없이 π bond만 가질 수 있는지, F2가 왜 그토록 reactive 한 지(bond order=1) 설명할 수 있다.
orbital의 에너지는 photoelectron spectroscopy (PES) 를 통해 직접적으로 측정할 수 있다. 입사된 광자의 에너지에서 튀어나온 electron의 kinetic energy의 차이가 ionization energy 이다. Ultraviolet lights은 주로 outer electrons을, X-rays는 주로 inner electron을 제거할 때 사용한다.
위 PES stpectrum에서 N2와 O2의 σg(2p)와 πu(2p)의 에너지가 역전되어 있는 것도 볼 수 있다.
PES spectrum에서 electronic energy의 vibration energy와의 상호작용도 볼 수 있다. vibrational energy간의 energy level은 electronic energy 보다 훨씬 작기 때문에, electronic level간의 transition은 vibraional level간의 transition 또한 포함하게 되어, multiple peaks로 나타나게 된다. bonding에 밀접하게 관여하는 orbital일 수록 vibrational fine peaks (multiple peaks)를 나타내게 된다.
Polar Bonds
Heteronuclear diatomic molecules의 경우에는 서로 다른 nuclear charge를 가진 atom이 bond를 형성하고 있다. 각각의 오비탈 에너지가 다르기 때문에 MO를 형성했을 때 각 atom의 AO의 MO에 대한 기여도 달라지게 된다. 한 atom의 AO가 MO의 에너지가 더 가깝다면 해당 MO에 더 많은 기여를 하게 되고, 더 큰 coefficeint를 갖는다. 일반적으로 AO orbital의 에너지가 12 or 13 eV 이상 차이가 나게되면 거의 상호작용하지 않는다고 생각한다.
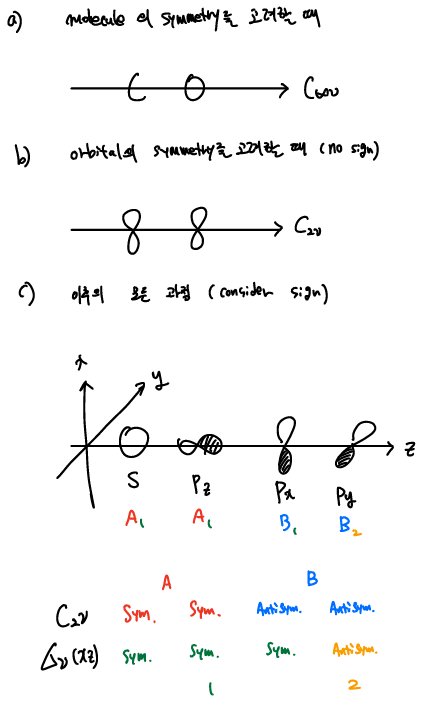
CO의 경우를 예로들어 보자. 먼저 주의할 점은 CO는 C∞υ symmetry를 가지고 있지만, 우리는 MO의 형성에 대해서 이야기 하고 있기 때문에 orbital의 symmetry를 고려해야한다. orbital lobe의 sign을 무시한다면, px와 py는 C2υ symmetry를 가지는데, orbital의 point group을 결정할 때만 sign을 무시하고 이후의 과정에 대해서는 모두 고려 해야 한다.
s와 pz orbital은 A1 (or a1) symmetry를 가지고, σ symmetry를 가진 MO를 형성한다. 반면, px와 py는 각각 B1, B2 or (or b1, b2) symmetry를 가지고 π symmetry를 가진 MO를 형성한다.
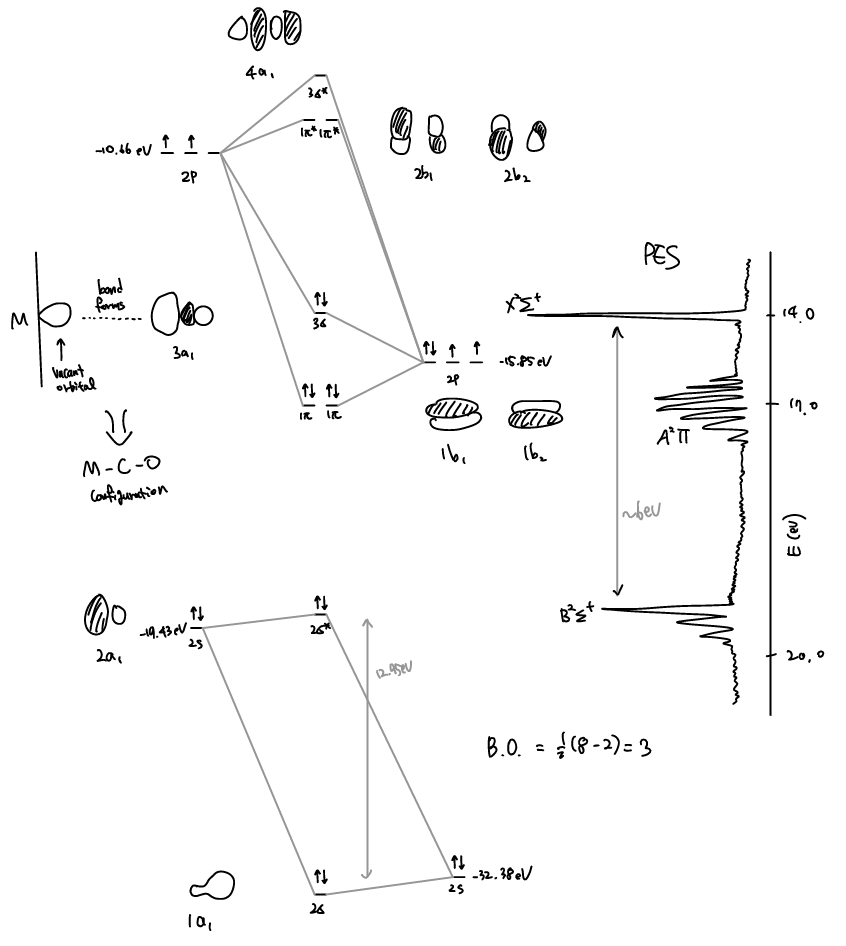
C 2s와 O 2s는 이미 ~ 13 eV 정도차이가 나기 때문에 MO를 형성할때 큰 interaction이 없을것이라 예상할 수 있다. 실제로 2σ orbital은 O 2s AO과 매우 가깝고, 2σ* 은 C 2s와 매우 가까운 것을 볼 수 있다. 반면 C 2p와 O 2p는 ~ 5 eV 정도 차이가 나므로 보다 강한 interaction이 가능하고 3σ이 어느정도 중간 값에 위치하는 것을 볼 수 있다. 3σ MO의 경우 orbital의 모양을 보면 C의 contribution이 더 커서 C 쪽의 orbital이 더 큰 것을 볼 수 있다 (bigger coefficient). 단순히 Electronegativity만으로 설명을 하려고 하면 이것을 이해가 되지 않는데, MO theory에서는 O 2p orbital의 경우 2σ* ( ,3σ, 3σ* ) 와도 상호작용이 가능하지만, C 2p의 경우엔 3σ 와 3σ* 에만 크게 기여하기 때문에 이와 같은 현상을 설명할 수 있다. 이것은 특히 Metal (M)과의 결합을 설명하는데 있어 매우 중요한데, CO의 3σ MO는 C 쪽에 더 많은 electron이 있기 때문에 O 보다는 C 가 M의 비어있는 orbital과 더 많이 상호작용하게 되고 따라서 M-O-C가 아닌 M-C-O의 binding mode를 갖게 된다.
Ionic Compounds
electronegativity의 차이가 극도로 많이 날 경우에는 electron이 more electronegative한 원자로 완전히 전달되고, 높은 에너지를 가진 양이온의 orbital은 비어지게 된다. 하지만 MO theory에서는 이러한 ion pair 또한 covalent compound로 고려될 수 있다.
MOs for larger molecules
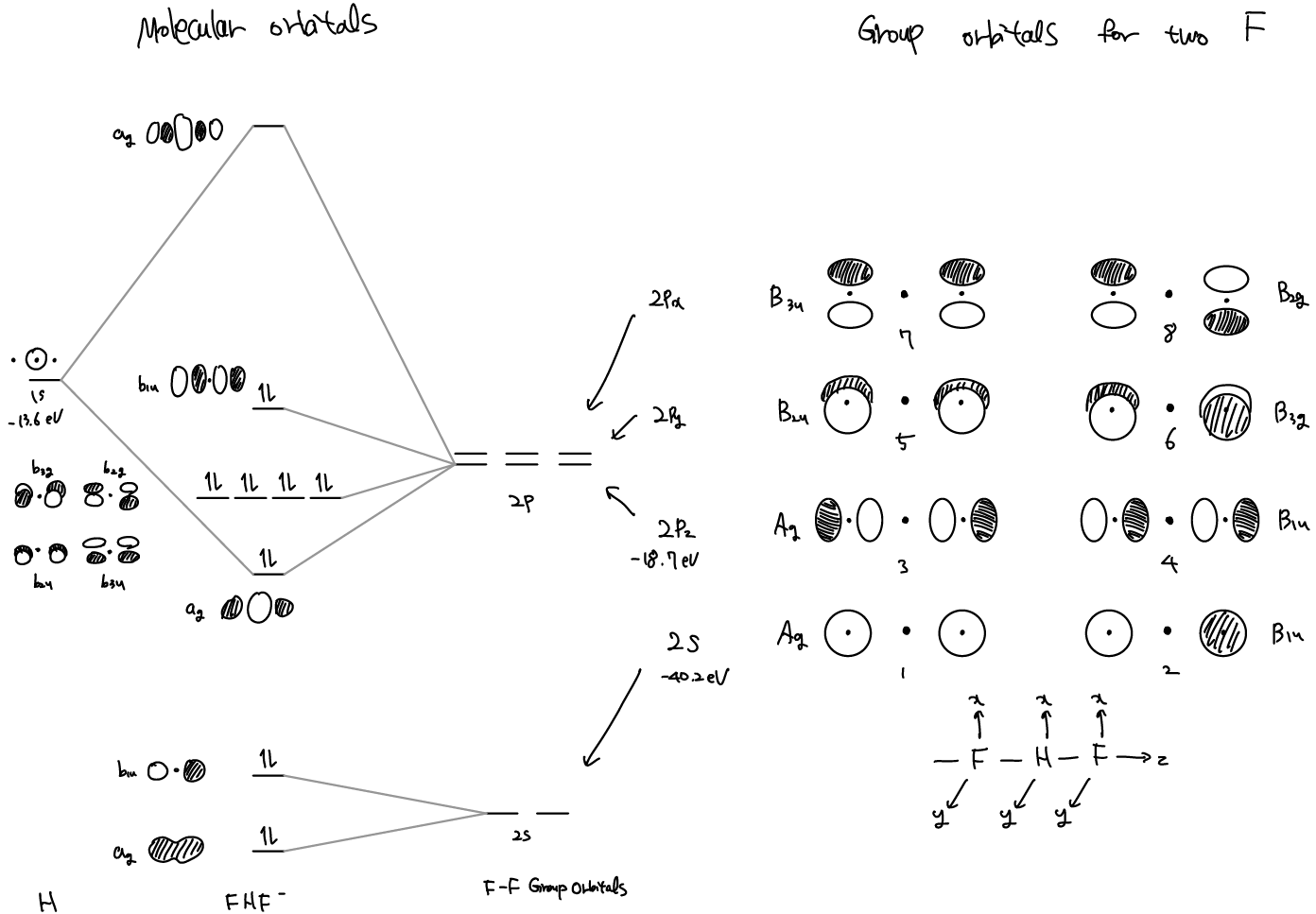
group orbitals (GO) the symmetry-adapted linear combinations (SALCs) or the orbital은 irreducible representation이 같은 atomic orbital의 linear combination이다. Molecular orbital은 molecule 전체를 나타내는 반면, orbital은 단순히 symmetry가 비슷한 orbital의 모음으로 bonding을 꼭 기술한다고 할 수는 없다. 아래의 FHF-의 예에서는 두 F 원자가 이루는 group orbital과 center의 H 1s orbital이 molecular orbital을 이룬다.
FHF-
FHF-는 매우 강한 hydrogen bonding을 이루고 있는 linear ion이다. Lewis 구조로 이를 표현하면 H 주위에 4개의 전자가 분포하게 되어버리기 때문에, MO theory를 통해 이를 쉽게 설명할 수 있다.
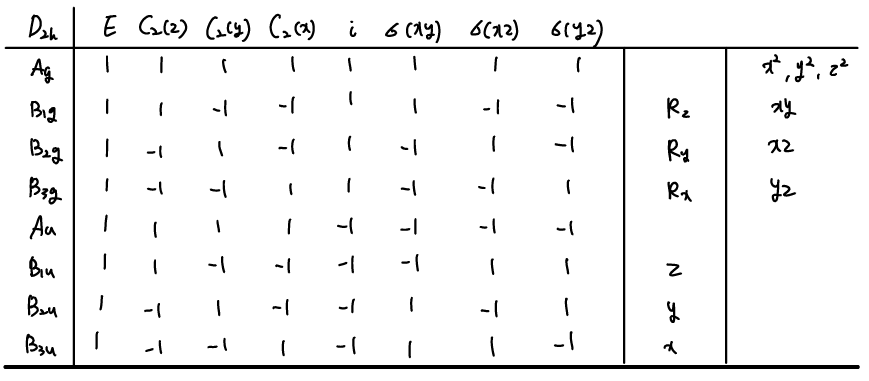
FHF-는 비록 D∞h point group을 가지고 있지만, infinite rotation axis는 다루기 어려우므로 D2h를 사용한다. D2h의 character table은 coorodinate axis 뿐만 아니라 orbital의 symmetry도 보여준다. 예를 들면 B1u는 F pz orbital과 z axis의 symmetry를 담고 있다. D2h의 irreducible representation 중 B1u를 보면, E, C2(z), σ(xz), σ(yz) operation에 대해 변화가 없고, C2(y), C2(x), i, σ(xy) operation에는 sign을 바꾸는 것을 알 수 있다.
위의 그림 오른쪽에 두 F 원자의 2s, 2p orbital로 이루어진 GO나타내었는데, diatomic molecule의 경우와 비슷하지만 central H atom으로 분리되어 있다. 각 GO의 symmetry는 character table에 나와있는 irreducible representation의 operation을 적용해보면 쉽게 찾을 수 있다. symmetry label을 보면 subscript가 3 인것도 볼 수 있는데, character table을 잘 보면, x, y에 대한 것임을 알 수 있다. (숫자 subscript은 principal axis에 수직인 C2에 대해 symmetric이면 1, antisymmetric이면 2 였다.)
H의 atomic orbital과 두 F의 GO를 결합한 molecular orbital을 왼쪽 그림에 함께 나타내었는데, H 1s (-13.6 eV)의 경우 F 2pz (-18,.7 eV)와 상호작용이 가능하지만, F 2s (-40.2 eV)와는 큰 에너지 차이 때문에 어렵다.
두 개의 F 원자로 만든 GO는 2 * 3 = 6 개이고, 수소 1와 결합하여 7개의 MO를 형성한다. 여섯개의 GO중 다섯개는 orbital symmetry가 맞지 않아 H 1s와 non-bonindg 으로 남게되고, lone pair electrons 가진다.
Lewis 구조와는 달리 MO theory에서는 3개의 atomic center에 delocalized 된 MO에 2개의 전자가 채워져 bond를 이룬다.
일반적으로 더 많은 atom에 걸쳐있을수록, 즉 더 큰 MO일수록 에너지가 낮다.