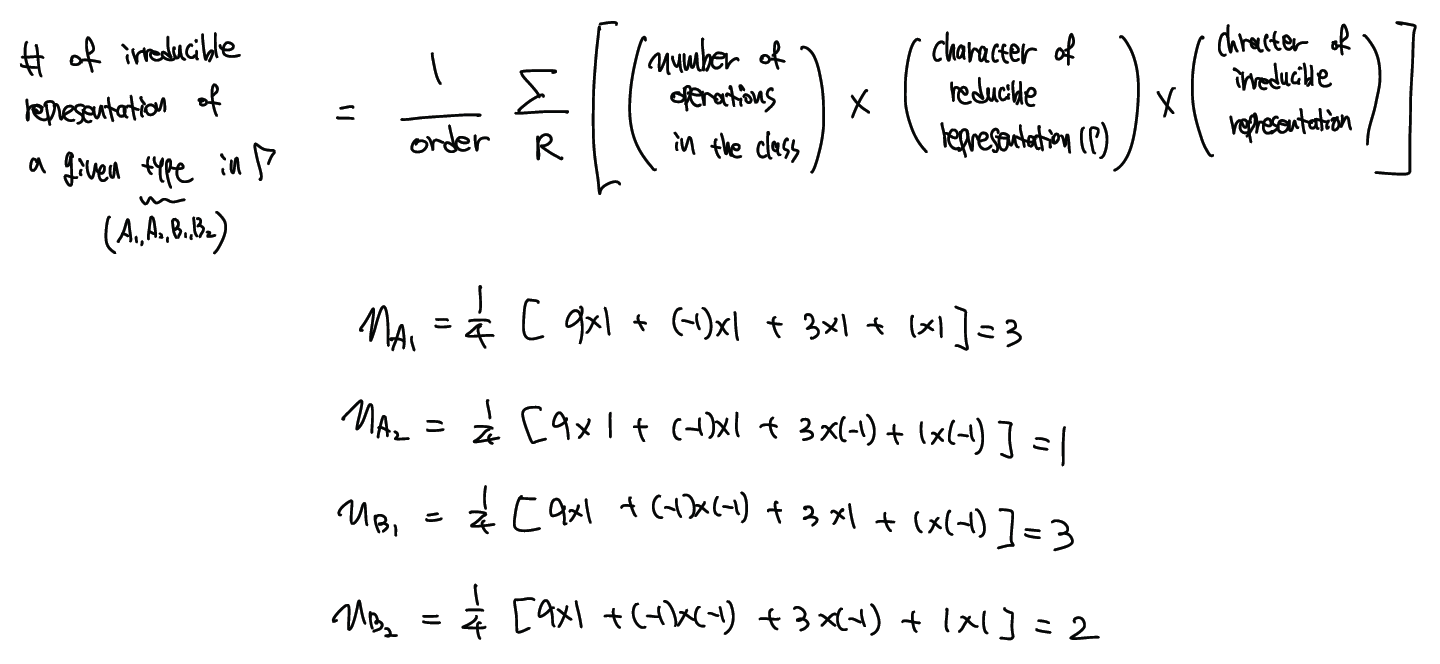Optical activity
Chirality
Mirror image에 중첩되지 않는 분자들을 chiral 또는 dissymmetric 하다고 한다. (dissymmetric 하다는 말이 곧 symmetry가 없다는 말은 아니다.) CBrClFI와 같은 분자처럼 E를 제외한 다른 symmetry operation이 없거나, only proper roation axis만 있을 때 그 분자를 chiral 하다고 말한다. 이러한 chiral 분자들은 빛을 편향시키는 성질이 있어 optical activity 가 있다. 빛을 시계방향으로 편향시키면 dextrorotatory, 반시계방향으로 편향시키면 levorotatory라고 한다.
Molecular Vibrations
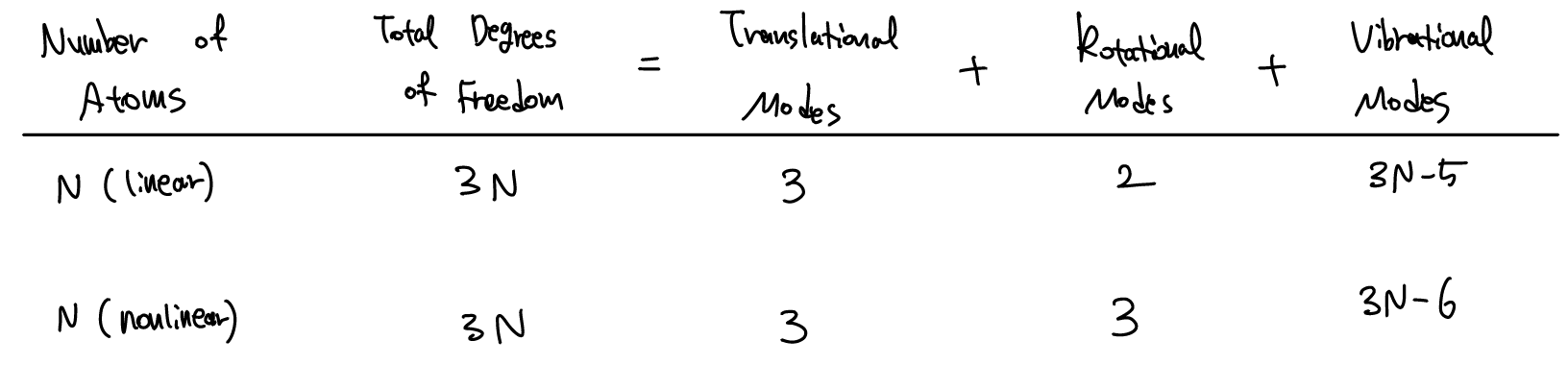
Vibration은 분자내 개개 원자의 motion에 관한 것이기 때문에 각 원자마다 x,y,z coordinate을 부여해야한다. 따라서 N개의 원자가 포함된 분자는 3N개의 degrees of freedom을 가진다. Degree of freedom의 수는 보존되어야 하므로,
Total Degree of freedom = Translational mode + Rotational mode + vibrational mode
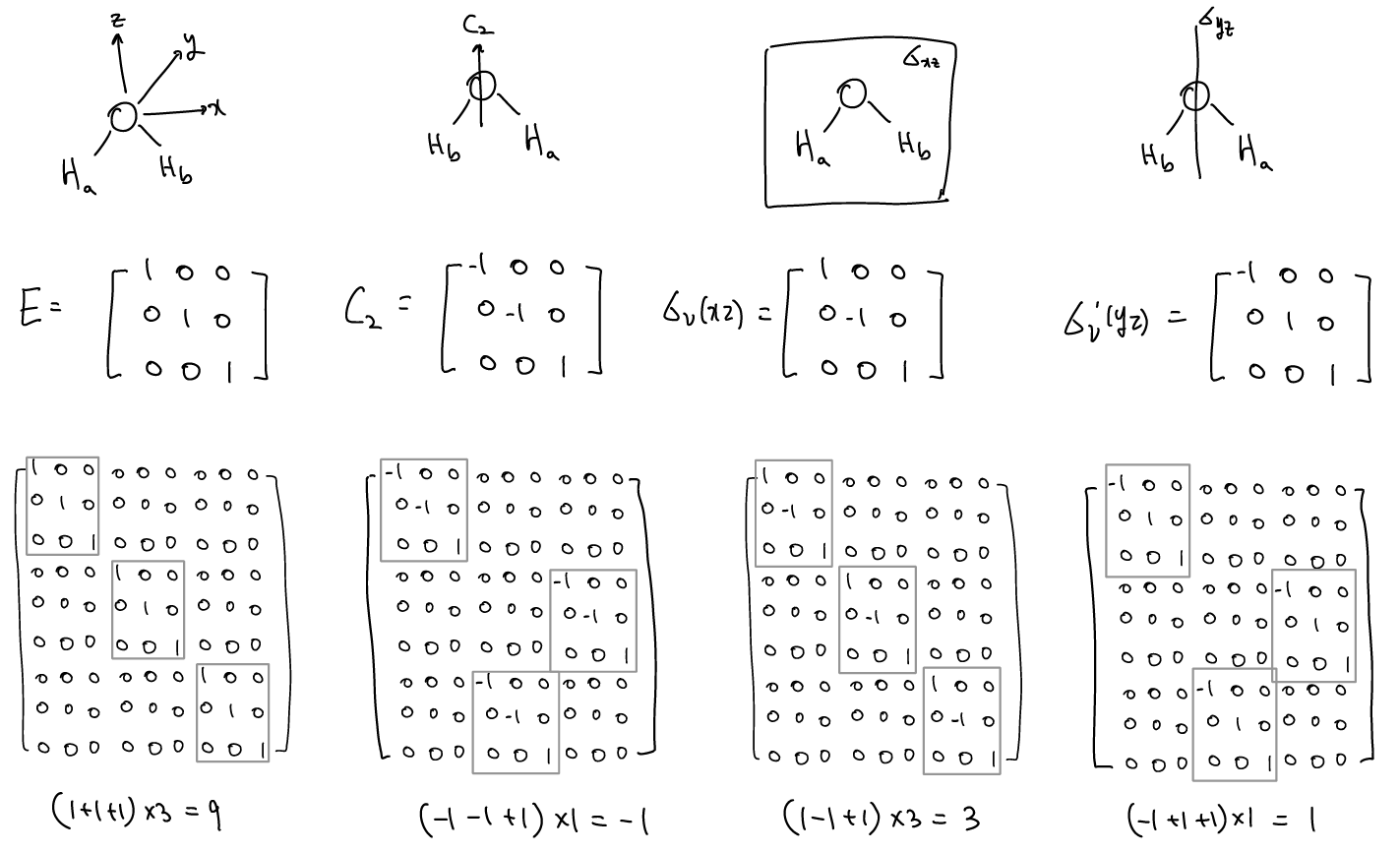
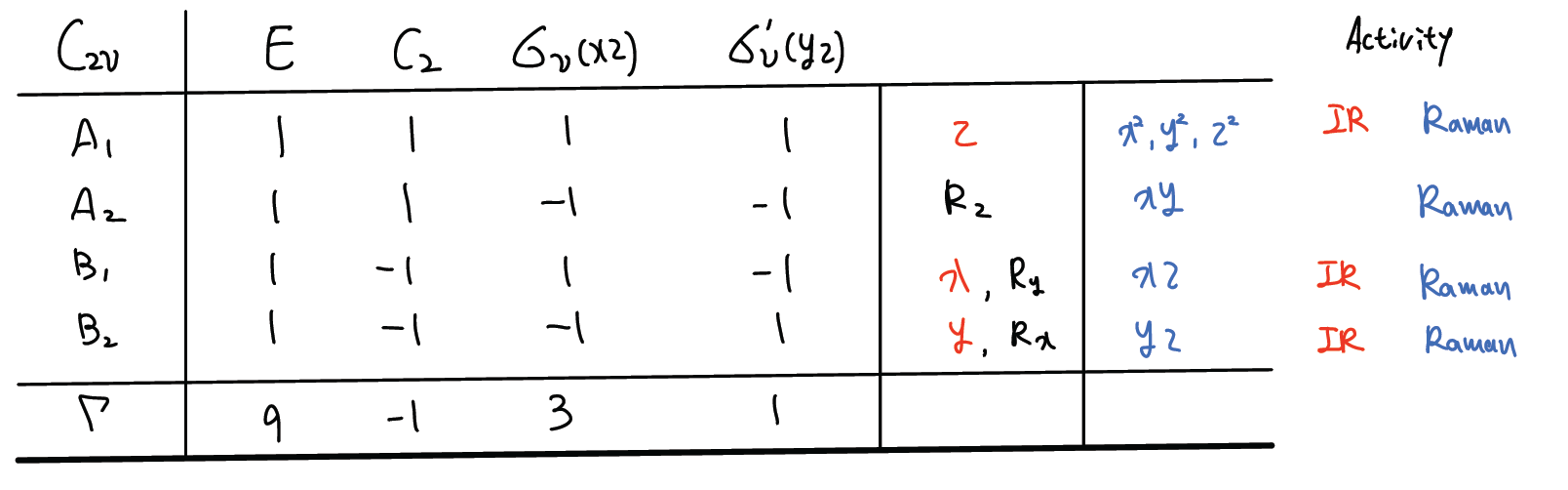
H2O(C2υ)는 9 개의 degree of freedom을 가지고 있다. C2υ의 symmetry operation은 4개가 있는데, 9개의 motion에 대해 translation, rotation, and vibration을 할당하기 위해서는, 9개의 motion이 몇개의 irreducible representation으로 표현될 수 있는지 알아보아야 한다. 이후에 각 irreducible representation의 symmetry가 어떠한 함수(xyz or RxRyRz)로 표현될 수 있는지 알아야 한다.
H2O의 경우 9x9 matrix여야 하나의 transformation matrix 를 표현할 수 있는데, C2υ는 아래의 symmetry operation은 4개가 있다. 9x9 matrix에서 C2υ나 συ(yz)처럼 Ha와 Hb의 위치가 서로 교환되는 경우에는 다음과 같이 3x3 block의 위치를 바꿔주어 교환을 표현한다. 이 경우에는 해당 block이 전체 matrix의 diagonal에서 벗어나므로 character를 결정할때는 기여가 0이 된다. 반면 E나 σ′υ(xz)처럼 위치에 변함이 없는 경우에는 모두 diagonal에 위치하여 character를 결정할 때 기여한다.
따라서 reducible representation (Γ)는 9 -1 3 1 이 된다. 이것은 9개의 motion 전체를 나타내는 하나의 지표라고 생각할 수 있다. 이 9가지의 motion을 각각의 irreducible representation의 요소로 분리하기 (or projection) 위해서 다음과 같은 규칙을 사용한다.
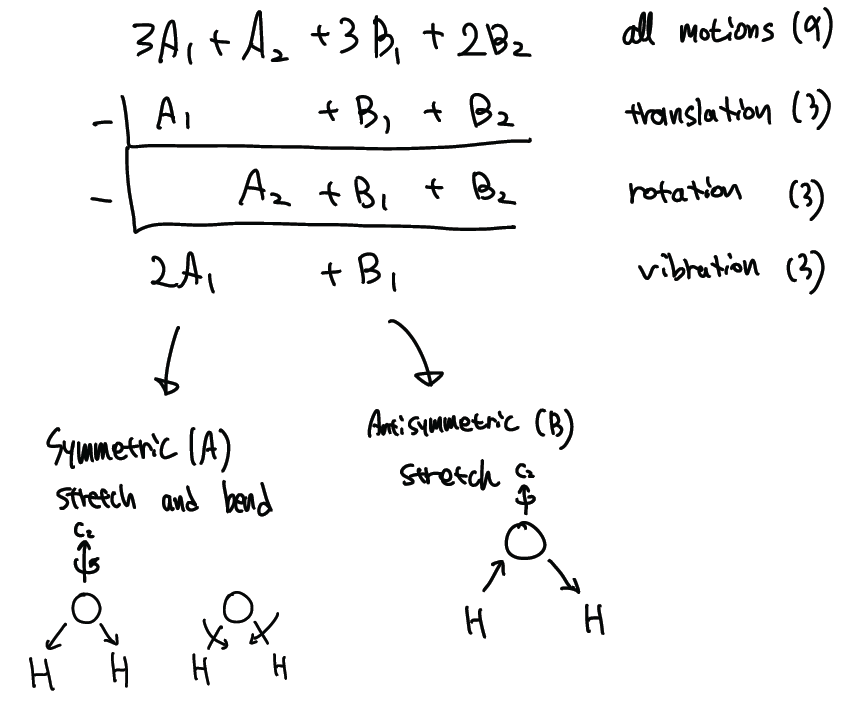
따라서 9개의 degree of freedom이 있기 때문에, 9개의 irreducible representaion이 있다. ( 3A1 + A2 + 3B1 + 2B2 ) 여기서 translation과 rotation motion의 갯수를 빼주어야 몇 개의 vibration mode가 있는지 알 수 있다.
아래 character table의 오른쪽을 보면 symmetry의 수학적 표현이 x, y, z coordination과 관련되어 있는지 Rx, Ry, Rz 같은 rotation axis와 연관되어 있는지 알 수 있다.
Translation은 x, y, z 와 관련되어 있으므로, A1, B1, B2가 이에 해당되고, Rotation은 Rx, Ry, Rz와 관련되어 있으므로, A2, B1, B2가 해당 된다.
따라서 이에 해당하는 만큼 Total degree of freedom에서 빼주면,
Vibration mode는 2A1 + B1만 남게된다. 즉 총 3개의 normal mode가 존재할 수 있다. 물론 irreducible representation이 해당 normal mode의 모든 것을 보여주진 않지만, 이러한 방법을 통해서 적어도 몇개의 vibration degree of freedom 이 있고 (symmetry label을 통해) 각각의 mode가 어떤 특징을 가지는지는 알 수 있다.
IR activity
Molecular vibration이 IR active하기 위해서는 해당 분자의 dipole moment의 변화가 있어야 한다.
Group theory에서는 vibrational mode가 IR active하려면 cartesian coordinates, x, y, or z에 대해 symmetry를 가지고 있어야 한다. 왜냐하면 x, y, or z 방향에 대해 분자의 center of charge가 이동하면 dipole moment를 형성하기 때문이다.
주의 할 점은 C2υ point group이라고 해서 위의 모든 IR active mode를 가지지 않는다는 점이다. H2O의 2A1 + B1 는 모두 IR active 하지만 B2 vibrational mode는 없다.
Raman activity
Molecular vibration이 Raman active하기 위해서는 해당 분자의 polarizability의 변화가 있어야 한다. Raman의 경우에는 vibration의 symmetry가 x, y, or z의 product (such as x2 or yz)의 함수로 표현 되어야 한다.