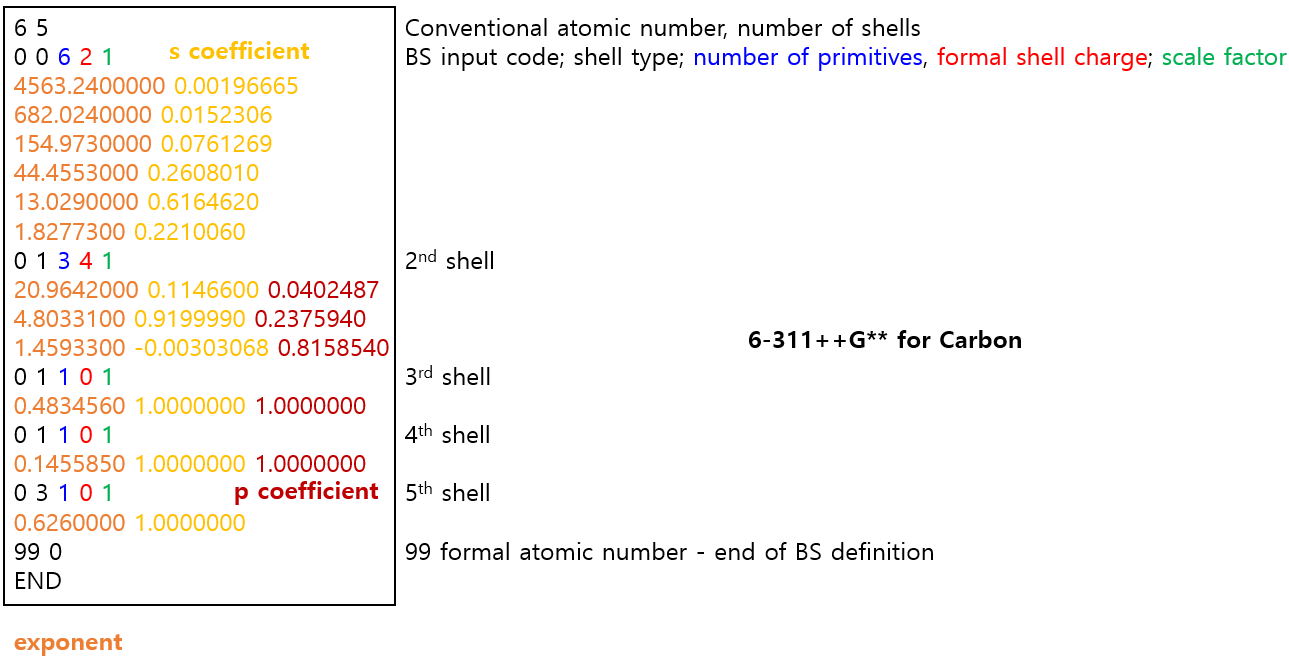
Basis set
CRYSTAL17, C, 6-311G++** example
- exponent가 너무 작은 diffuse function 하나 제거함.
- CRYSTAL17 INPUT 만들때, center of mass를 origin으로 맞추지 않아서, symmetry operation 중에 구조가 망가졌었음… 아 개고생…
- Formal Shell Charge는 임의로 정해도 되는 듯. Check O in NiO vs CoO case J. Phys. Chem. Lett. 2016, 7, 1198. 다만, Neutral charge를 만족하기 위해서는 다른 element의 Charge도 바꿔야 함. 뭐든, 수렴이 잘 되는 쪽을 선택하면 될 듯 as a initial electron density.
Hybrid DFT [4]
Perioidic system에서는 one particle orbitals (crystalline orbitals)이 a crystal quasi-momentum index (k) in reciprocal space로 표기된다. CRYSTAL에서는 atom centred atomic orbitals (AOs, phi)의 linear combination으로 표현된다.
\(\psi_{i}(\vec{r} ; \vec{k})=\sum_{\mu} a_{\mu, i}(\vec{k}) \sum_{g} \phi_{\mu}\left(\vec{r}-\vec{A}_{\mu}-\vec{g}\right) e^{i \vec{k} \cdot \vec{g}}\)
A_mu는 핵의 coordinate, g는 direct space lattice vector, a는 crystall oribital in the AO basis의 expansion coefficient. 이 coefficient는 SCF equation을 풂으로써 결정된다. 각각의 AOs는 각각 nomalized된 Gaussian type functions (GTFs, G)의 linear combination으로 표현된다.
\(\phi(\vec{r}-\overrightarrow{A_{\mu}}-\vec{g})=\sum_{j}^{n_{G}} d_{j} G\left(\alpha_{j} ; \vec{r}-\overrightarrow{A_{\mu}}-\vec{g}\right)\)
이렇게 AOs들의 집합을 basis set이라고 부르게 된다.
HF든 DFT든 a는 아래와 같은 k-dependent Roothan-Hall like equation을 풀어서 결정한다.
\(H(\vec{k}) A(\vec{k})=S(\vec{k}) A(\vec{k}) E(\vec{k})\)
여기서 S는 overlap matrix, E는 (diagonal) matrix of eigenalues.
Band energy는 다음과 같이 direct space에서 Hamiltonian matrix의 Fourier transform으로 표현한다.
\(H(\vec{k})=\sum_{\vec{g}} H^{\vec{g}} e^{i \vec{k} \cdot \vec{g}}\)
Total energy는 다음과 같다.
\(E_{t o t}=\frac{1}{2} \sum_{i j} \sum_{\vec{g}} P_{i j}^{\vec{g}} H_{i j}^{\vec{g}}\)
reference
[1] Introduction to Computational Chemistry
[2] Basis Sets in Quantum Chemistry
[3] Background Reading for Basis Sets
[4] Removing pseudo-linear dependence in Gaussian basis set calculations on crystalline systems with the CRYSTAL code