Kronig-Penney Model
Python code, kronigPenney.py
Numerical matrix method for quantum periodic potentials
값을 넣어서 변화를 보자.
Allowed and forbidden energy band가 어떻게 형성되는지 살펴보자.
아래 그림과 같이 반복적으로 이루어진 array of square-well potentials 생각해보자.
Allowed energy를 찾기 위해서는 V=0인 구간과 V=V0인 구간에서 따로따로 슈뢰딩거 방정식을 푼뒤에 파동함수의 연속성과 주기성을 만족하도록 적절한 경계조건을 적용한다.
V=0 인 구간에서의 해는
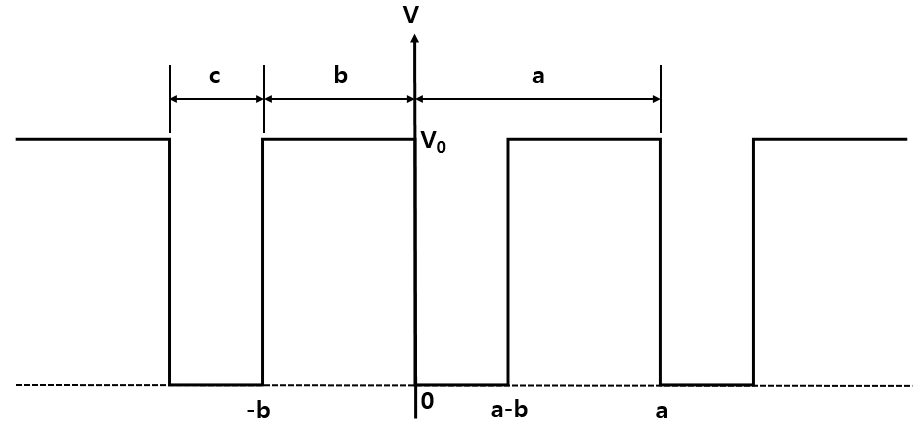
\(\psi_{0}=\operatorname{Aexp}(i \beta x)+\operatorname{Bexp}(-i \beta x)\)
\(\beta=\frac{\sqrt{2 m E}}{\hbar}\)
V=V0인 구간에서의 해는
\(\psi_{v}=\operatorname{Cexp}(i \alpha x)+\operatorname{Dexp}(-i \alpha x)\)
\(\alpha=\frac{\sqrt{2 m\left(V_{0}-E\right)}}{\hbar}\)
연속성을 위한 조건과 x=0에서,
\(\psi_{0}(0)=\psi_{v}(0)\)
\(\left.\frac{\partial \psi_{0}}{\partial x}\right|_{x=0}=\left.\frac{\partial \psi_{v}}{\partial x}\right|_{x=0}\)
주기성을 위한 조건을 설정하면,
\(\psi_{v}(-b)=\exp (-i k a) \psi_{0}(a-b)\)
\(\left.\frac{\partial \psi_{v}}{\partial x}\right|_{x=-b}=\left.\exp (-i k a) \frac{\partial \psi_{0}}{\partial x}\right|_{x=(a-b)}\)
다음과 같은 energy restricting condition을 구할 수 있다.
\(\cos k a=\left[\frac{\alpha^{2}-\beta^{2}}{2 \alpha \beta}\right] \sinh \alpha b \sin \beta(a-b)+\cosh ^{-1} \alpha b \cos \beta(a-b)\)
여기서 아래의 조건을 만족하도록 barrier의 폭인 b가 0까지 감소할 수 있는 반면, 높이는 제한없이 증가할 수 있다고 가정해보자.
\(\mathrm{P}=\left(\frac{m a}{\hbar^{2}}\right) \mathrm{bV}_{0}=\mathrm{constant}\)
이것은 barrier의 넓이가 일정하다는 조건인데, 이를 통해 square potential well을 delta function으로 바꾸게 되면,
\((\mathrm{V}-\mathrm{E}) \rightarrow \mathrm{V}_{0}, \sinh \alpha b \rightarrow \alpha b, \cosh ^{-1} \alpha b \rightarrow 1\)
결국 다음과 같이 energy-limiting condition을 표현할 수 있다.
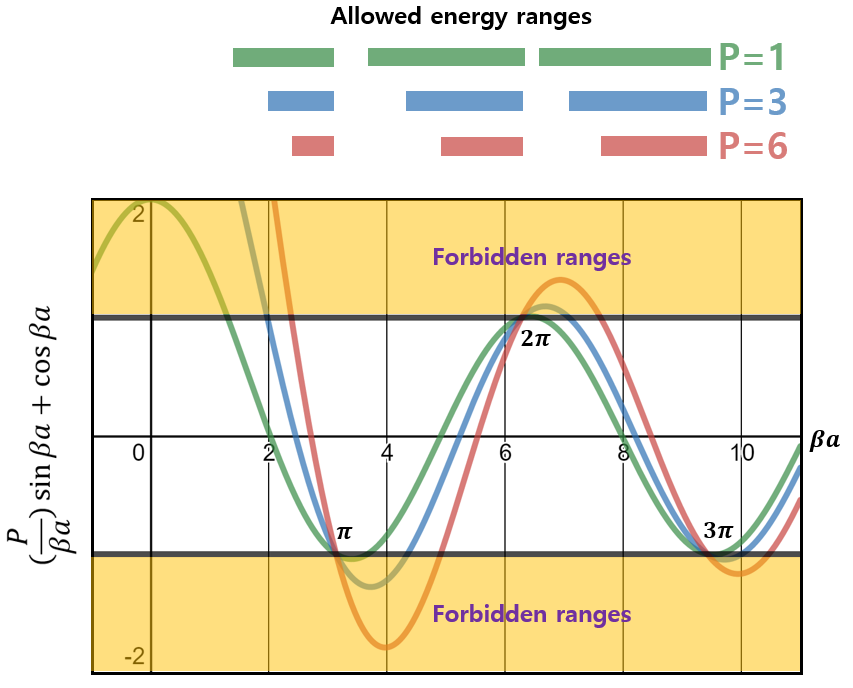
\(\cos k a=\left(\frac{P}{\beta a}\right) \sin \beta a+\cos \beta a\)
이때 -1 <= cos(ka) <= 1 이므로, βa가 가능한 범위가 정해지게 된다.
reference
[1] ELECTRONS IN SOLID An introductory Survey, Richard H. Bube, ISBN: 0-12-138650-3